| Home | Fotografische vormgeving | Tekeningen | Digigrafiek | Objecten | Boeken | Contact | Exposities | Additioneel | Info |

Donderdag 5 september t/m zondag 29 september 2013 | De Ploeg thema-expositie in de Koepelzaal van Academie Minerva te Groningen.

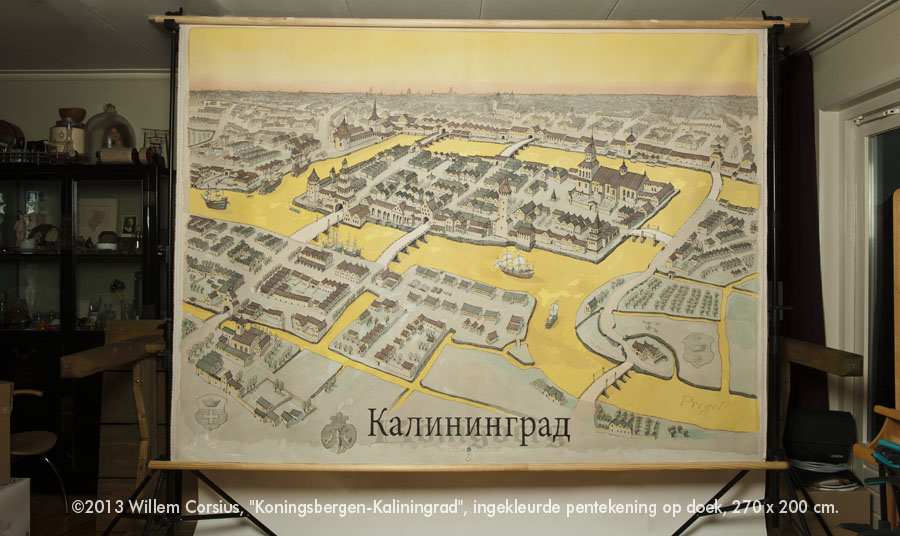
De zeven bruggen van Koningsbergen is een wiskundig vraagstuk.
Het vraagstuk De stad Koningsbergen (Kaliningrad) lag in het oosten van Pruisen aan de rivier de Pregel, waarin twee eilanden lagen die door zeven bruggen met elkaar en met de vaste wal verbonden waren. De vraag was nu of het mogelijk is om zó te wandelen dat je precies één maal over elke brug liep. In sommige versies van het vraagstuk werd ook geëist dat men terug bij het startpunt eindigde. In 1736 heeft Euler aangetoond dat dit onmogelijk is.
De huidige staat van de bruggen Twee van de zeven oorspronkelijke bruggen werden vernietigd door het bombardement op Koningsbergen ten tijde van de Tweede Wereldoorlog. Twee andere werden later door de Russen verwijderd en vervangen door een snelweg. De overige drie bruggen bestaan nog, waarbij opgemerkt wordt dat er slechts twee dateren uit de tijd van Euler, en dat er één door de Duitsers in 1935 werd herbouwd. Daarmee is op dit moment een Eulerwandeling wel degelijk mogelijk, alhoewel het voor toeristen een onpraktische route zou zijn.